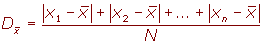MEDIDAS DE DISPERSION
Medidas de dispersión. Son parámetros estadísticos que
indican como se alejan los datos respecto de la media aritmética. Sirven como
indicador de la variabilidad de los datos. Las medidas de dispersión más
utilizadas son el rango, la desviación estándar y la varianza.
Rango
Indica la dispersión entre los valores extremos de
una variable. se calcula como la diferencia entre el mayor y el menor valor de
la variable. Se denota como R.
Para datos ordenados se calcula como:
R = x(n) - x(1)
Donde: x(n): Es el mayor valor de la
variable. x(n): Es el menor valor de la variable.
Por ejemplo:Estas dos series: Serie 1:
1 5 7 7 8
9 9 10 17 ( R =17-1=16) Serie 2: 2 4
6 8 10 12 14 16 18 ( R =18-2=16) Ambas
series tienen rango 16, pero están desigualmente agrupadas, pues mientras la
primera tiene una mayor concentración en el centro, la segunda se distribuye
uniformemente a lo largo de todo el recorrido. El uso de esta medida de
dispersión, será pues,
bastante restringido.
Varianza
La varianza (S2) mide
la dispersión de los datos de una muestra respecto a la media,
calculando la media de los cuadrados de las distancias de todos los datos.
Al elevar las diferencias al cuadrado
se garantiza que las diferencias absolutas respecto a la media no se anulan
entre si. Además, resaltan los valores alejados.
Siempre se cumple que la varianza
es mayor o igual que cero (S2 ≥ 0). La varianza es cero
cuando todos los datos son el mismo (ejemplo: {1,1,1,1,1}).
Si en vez de tratarse de una muestra,
la varianza se refiere a la población, el denominador será N.
Desviación media
La desviación respecto a la media es la diferencia
entre cada valor de la variable estadística y la media aritmética.
Di = x - x
La desviación media es la media
aritmética de los valores absolutos de las desviaciones respecto a la
media.
La desviación media se representa por D
Por ejemplo: Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Para saber mas hagan clic en el siguiente enlace:
http://www.universoformulas.com/estadistica/descriptiva/medidas-dispersion/
Espero que disfruten el siguiente video
Gracias por su atención
Elaborado por: Laura Nayeli Fabian Martinez